Unicursal polygram

I worked out on unicursal pattern on polygram and found that the sequence does not exist for distinct patterns excluded differential on orientations and reflections.
The sequence showed as following:
n          unicursal pattern
3                     1
4                     2
5                     4
6                   12
7                   36
8                 162
9                 648      Forecast from OEIS A007694 
10             2592      Forecast from OEIS A007694
11           11664      Forecast from OEIS A007694
12           46656      Forecast from OEIS A007694    
. . . . . . . . . . . . .

What are number of unicursal pattern for n > 8 ?

I found some pattern of fibonacci sequence in web.

The hidden pattern of magic number is quite beautiful.

Fibanacci * x mod m

found discussion on 3-6-9 on web, if x3 to fibonacci sequence and reduce to single digit or mod 9
the result is octave of "3-3-6-9-6-6-3-9" or "3-3-6-0-6-6-3-0" by modulo method which 0=9, no remainder.
I try to vary multiplier (x) from 2-24 amd m = 9, 11, 12
The pattern of numbers appearance frequency are symetry and beautiful.

Fibonacci Mod 12 R2

Afetr consider pisano period on pi(m)=24, mod 9 have number 1 & 8 apprear 5 time
also mod 12 , 1 & 5 appesr 5 time. This should be beautiful pattern hidden in mod 12 as well.
Today I found such pattern...

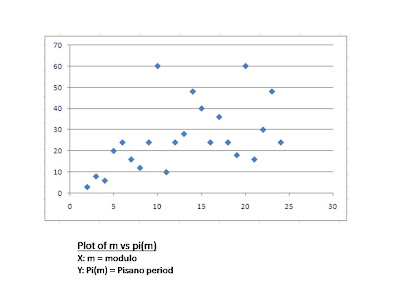
Fibonacci Pisano Pattern

from pisano period up to m=24.
for m=2,4,11,19,22    there are no zero in the middle of cycle.
there are reverse sequences of 1,2 ,3.......as mark by bold block
there is clearly trand of some data.

Fibonacci Mod 12

After rework on pisano mod n up to 24, I try to draw N-gram mod 11 but not found beautiful pattern.
I relook to mod 12, it has 5 symetrical patterns by using the same method of mod 9 enneagram

Pythagoras Triplet

From a^2 + b^2 = c^2
If a = prime, then c = b+1, or p^2 + b^2 = (b+1)^2
If a not prime, b & c shall be prime except: 3 set of triplet (for first 100 number)
i.e. 56, 33, 65
      63, 16, 65
      77, 36, 85

The plot of p & a is highly correlation.
But the plot of a & b for non-prime quite scatter.